CURVE25519
ELLIPTIC CURVE CRYPTOGRAPHY: CURVE25519
Table of content:
- Introduction
- The Curve25519
- The Montgomery Ladder Algorithm
- Generating the Private key and Public key
- Conclusion
Introduction
Curve25519 or X25519 is an Elliptic Curve Cryptography (ECC) Algorithm designed by Daniel J. Bernstein and was introduced in 2005. The purpose of X25519 is for fast and secure key exchange. ECC uses the mathematics of elliptic curves over a finite field. Some key feature of the X25519:
- Efficiency
- Compact representation
- Immune to timing attack
- Ease of implementation
- Uses the Diffie-Hellman Key Exchange
I already have some blog in ECC and Finite field.
The Curve25519
Look at my previous blog about ECCs to know the mathematics behind it.
The Montgomery Ladder Algorithm
The curve25519 uses scalar multiplication to generate the public key using the private key and the base point. The algorithm used to calculate the scalar multiplication is the Montgomery Ladder Algorithm.
The Montgomery Ladder Algorithm uses the adding points and doubling points arithmetic that Elliptic curves have.
Here is the logic behind it. Below is a pseudocode of the algorithm:
-----------------------------------------------------------------------------------------------------------------------------
//Initialise the 2 points R0 and R1
R0 = (0,1)
R1 = BasePoint
//get the length of the binary of scalar
bit_length = scalar.BIT_LENGTH(Scalar)
FOR I <-- Bit_length -1 TO -1 STEP -1
//Get the i-th bit in the binary
bit_i = (scalar >> i ) & 1
//Select point based on the i-th bit
IF (bit_i = 0) THEN
R1 = AddPoints(R0, R1)
R0 = DoublePoint(R0)
ELSE
R0 = AddPoints(R0, R1)
R1 = DoublePoint(R1)
ENDIF
RETURN R0
END FUNCTION
-----------------------------------------------------------------------------------------------------------------------------
On my blog, Elliptic Curve: Montgomery Curve, I already explained the point addition and point doubling in great details with an example.
Generating the Private Key and Public Key
To compute the public key, we use the equation:
The equation uses scalar multiplication to compute the Public key. The Montgomery Ladder Algorithm can perform the Scalar Multiplication.
Here is my version of the pseudocode of the generation and computation of the public and private keys:
-----------------------------------------------------------------------------------------------------------------------------
//Global Parameters
prime_mod = POWER(2, 255) - 19
//By^2 = x^3 + Ax^2 + x
A = 486662
B = 1
BasePoint = (9, 14781619447589544791020593568409986887264606134616475288964881837755586237401)
//Generate the Private Key
PrivateKey = RANDOM.INTEGER(1, 2^252 + 27742317777372353535851937790883648493)
//Generate public key
PublicKey = Montgomery_Ladder(BasePoint, PrivateKey)
//Encoding the public key to a standard version
Encoded_PublicKey = Encode(PublicKey)
PRINT("Private key: ", PrivateKey)
PRINT("Public key: ", PublicKey)
//HEX() display the hexadecimal Version
PRINT("Public key: ", Encoded_PublicKey.HEX())
-----------------------------------------------------------------------------------------------------------------------------


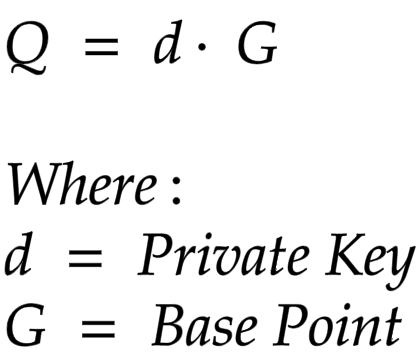

Comments
Post a Comment