Elliptic Curve: Montgomery Curve
Montgomery Curve
Table of Content:
- Definition
- Montgomery Arithmetic
- Addition
- Doubling
- Examples
- Conclusion
Definition
Next blog am going to touch on Finite Field in Montgomery Curve.
Montgomery Arithmetic
There are two type of Arithmetic in this type of Curve:
- Adding: It consist of adding 2 points to find the third point.
- Doubling: It consist of 1 point to find the other.
Addition
So:
Using P1 and P2, we can find the equation of the line, L.
2. To find the third point, we can take both the equation and find the third intersection point.
The result is an equation with third degree. Since it is a third degree equation, it should have 3 solution. It can be rewritten as:
Lets expand the brackets:
Lets analyze:
Lets look at the second degree (x^2). it show that:
We get the value of x3. We can then replace this value in either the Curve or the straight line to get the y3 (y-coordinate of P3).
Doubling
In doubling, the line only touches 2 points, P1 and P3. Given point P1, [2]P1 represent geometrically the third point of intersection between the line and curve. So to find the coordinate of P3, we use the equation P3 = [2]P1. We can use the same approach as addition with the exception that the line touches at 2 points only. So to get the gradient at point P1, we must differentiate the curve.
Assuming:
Now we replace the x and y value by the coordinate of P1 to get the gradient of the line.
Examples
Addition
Doubling
Lets Differentiate the curve to get the gradient at P1.
Using the second degree derived equation:
Conclusion
Montgomery is an elliptic curve which is being used in the field of cryptography. The simple arithmetic produces the keys need for communication.
One thing that I did not touched on Montgomery is the Field of the curve. As the definition above states that a Montgomery curve has a field K. This will be on my next blog.

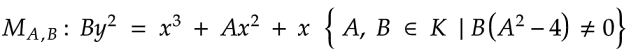





















Comments
Post a Comment